Pyt.1.
Wskaż fałszywą równość:
-
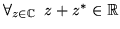
-
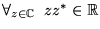
-
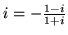
-
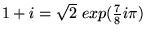
Pyt.2.
Współczynnik normalizacji N dla stanu cząstki w pudle
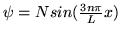 wynosi:
wynosi:
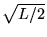
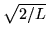
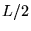
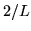
Pyt.3.
Operator Hamiltona dla układu składającego się z elektronu o masie 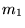 i
ładunku
i
ładunku 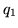 opisywanego przez wektor
opisywanego przez wektor
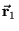 i protonu o
i protonu o
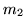 i
i 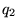 wskazywanego przez
wskazywanego przez
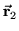 ma postać:
ma postać:
-
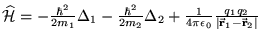
-
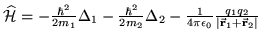
-
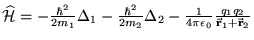
-
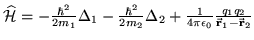
Pyt.4. Dla cząstki swobodnej:
- funkcja falowa jest kombinacją liniową fal płaskich
- operator Hamiltona
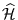 jest przemienny z operatorem
pędu
jest przemienny z operatorem
pędu 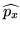 i nieprzemienny z
i nieprzemienny z
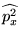
- poziomy energetyczne są skwantowane
- energia potencjalna zachowuje się jak
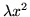 dla pewnego
dla pewnego 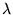
Pyt.5. Swobodna cząstka o energii E (obszar I) napotyka barierę potencjału o
wysokości V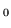 dla V
dla V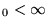 (obszar II). Prawdziwe jest:
(obszar II). Prawdziwe jest:
- jeśli E
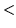 V
V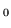 , to prawdopodobieństwo znalezienia cząstki w obszarze
II wynosi 0
, to prawdopodobieństwo znalezienia cząstki w obszarze
II wynosi 0
- dla E
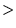 V
V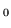 długość fali de Broglie'a tej cząstki
zmniejszy się w obszarze II
długość fali de Broglie'a tej cząstki
zmniejszy się w obszarze II
- dla E
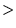 V
V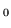 funkcja falowa cząstki w obszarze II
zanika jak
funkcja falowa cząstki w obszarze II
zanika jak 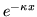 , gdzie
, gdzie
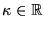
- efekt tunelowania do obszaru II nie zachodzi dla V
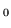 równego
równego 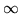
Pyt.6.
Jeżeli operatory 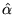 i
i 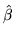 posiadają wspólny zbiór
funkcji własnych, to są:
posiadają wspólny zbiór
funkcji własnych, to są:
- ortogonalne
- hermitowskie
- przemienne
- nie istnieją takie operatory
Pyt.7. Ze wzrostem liczby numerującej stany dla cząstki w pudle potencjału o
szerokości L:
- zmniejsza się energia cząstki
- funkcja falowa ma coraz więcej węzłów
- zmniejsza się rozmiar pudła
- nie zmienia się odległość (energetyczna) pomiędzy sąsiednimi poziomami
Pyt.8. Ze wzrostem szerokości pudła potencjału L:
- funkcja falowa się nie zmienia
- rośnie odległość (energetyczna) pomiędzy sąsiednimi stanami
- energia stanów własnych
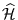 maleje jak
maleje jak 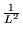
- zmiana szerokości pudła jest niemożliwa, gdyż wtedy funkcja falowa musi
przyjąć w każdym punkcie przestrzeni wartość 0
Edyta Malolepsza
2000-12-15