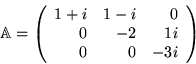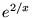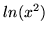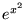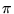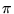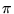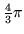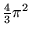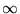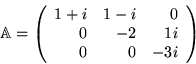- Wyznacznik macierzy
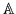 wynosi:
wynosi:
- 6i
- -1-2i
- -6+6i
- 6+6i
- Iloczyn skalarny wektorów: [-1,3,0] i [2,2,-4] jest równy:
- -6
- 4
- [-12,4,-8]
- [-2,6,0]
- Iloczyn wektorowy wektorów: [2,0,1] i [0,1,-1] wynosi:
- 2
- -1
- [-1,2,2]
- [0,0,-1]
- Pochodna wyrażenia
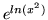 wynosi:
wynosi:
- 2x
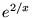
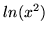
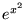
- Całka
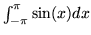 jest równa:
jest równa:
- -1
- 1
- 0
- -
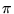
- Pole kuli o promieniu 1 wynosi:
- 2
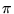
- 4
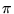
-
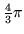
-
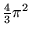
- Ile wynosi granica wyrażenia
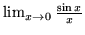 ?
?
- 0
- 1
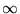
- nie istnieje
- Rzucamy 3 razy monetą idealną. Prawdopodobieństwo, że wypadną
w sumie dwa orły i jedna reszka jest równe:
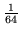
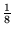
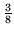
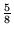
- Która z liczb podniesiona do kwadratu będzie równa
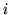 ?
?
-
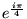
-
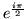
-
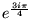
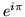
- Równanie różniczkowe
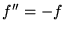 spełnia funkcja:
spełnia funkcja:
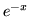
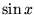
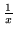
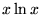
Edyta Malolepsza
2000-12-15