| a) pędu, | b) momentu pędu, |
| c) siły, | d) energii. |
| a) zjawisko fotoelektryczne, | b) zjawisko Comptona, |
| c) serie widmowe atomu wodoru, | d) dyfrakcja elektronów na kryształach. |
- a)
-
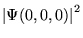 ,
,
- b)
-
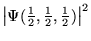 ,
,
- c)
-
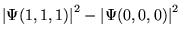 ,
,
- d)
-
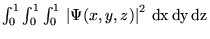 .
.
Które zdanie jest fałszywe:
- a)
- dla dowolnych
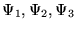 :
:
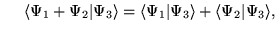
- b)
- dla dowolnych
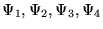 :
:
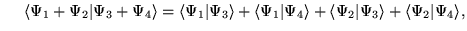
- c)
- dla dowolnych
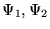 :
:
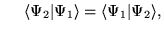
- d)
- dla dowolnych
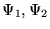 :
:

| a)
|
b)
|
| c)
|
d)
|
| a) |
b)
|
c)
|
d)
|
| a)
|
b)
|
| c)
|
d)
|
| a) znamy |
b) znamy |
| c) znamy |
d) znamy |