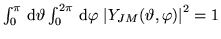- a)
- jest falą o długości większej niż na zewnątrz schodka,
- b)
- jest falą o długości takiej samej jak na zewnątrz schodka,
- c)
- jest falą o długości mniejszej niż na zewnątrz schodka,
- d)
- zanika eksponencjalnie.
| a) 140 |
b) 160 |
c) 200 |
d) 240 |
| a) |
b) |
c) |
d) |
| a)
|
b) |
c)
|
d) |
- a)
-
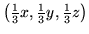
- b)
-
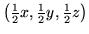
- c)
-
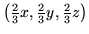
- d)
-
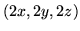
- a)
- taka sama energia, różne kwadraty momentu pędu,
różne składowe
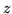 momentu pędu,
momentu pędu,
- b)
- taka sama energia, taki sam kwadrat momentu pędu,
różne składowe
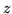 momentu pędu,
momentu pędu,
- c)
- różne energie, taki sam kwadrat momentu pędu,
taka sama składowa
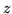 momentu pędu,
momentu pędu,
- d)
- różne energie, różne kwadraty momentu pędu,
różne składowe
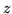 momentu pędu.
momentu pędu.
| a) |
b) |
c) |
d) |
- a)
-
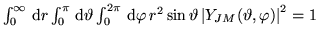
- b)
-
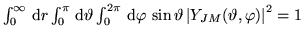
- c)
-
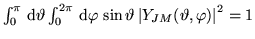
- d)
-