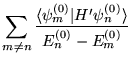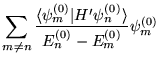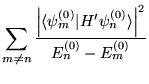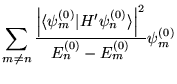- Energia stanu podstawowego pewnego układu wynosi
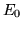 . Dla dowolnej
funkcji
. Dla dowolnej
funkcji 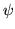 z przestrzeni Hilberta tego układu wartość średnia
hamiltonianu,
z przestrzeni Hilberta tego układu wartość średnia
hamiltonianu,
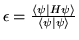 ,
spełnia warunek
,
spełnia warunek
- Szukamy metodą wariacyjną przybliżonej funkcji falowej stanu
podstawowego pewnego układu w klasie funkcji zależnych od jednego
parametru rzeczywistego
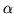 . Obliczyliśmy, że wartość średnia
hamiltonianu dla funkcji z tej klasy wynosi
. Obliczyliśmy, że wartość średnia
hamiltonianu dla funkcji z tej klasy wynosi
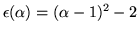 . Zatem przybliżona energia stanu podstawowego
jest równa
. Zatem przybliżona energia stanu podstawowego
jest równa
a) 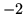 |
b) 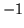 |
c) 1 |
d) 2 |
- Niech
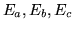 będą wariacyjnymi przybliżeniami do energii
stanu podstawowego atomu wodoru, otrzymanymi odpowiednio w klasach funkcji
próbnych
będą wariacyjnymi przybliżeniami do energii
stanu podstawowego atomu wodoru, otrzymanymi odpowiednio w klasach funkcji
próbnych
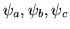 :
:
gdzie 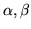 są (rzeczywistymi) parametrami,
są (rzeczywistymi) parametrami, 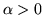 . Które
nierówności są prawdziwe:
. Które
nierówności są prawdziwe:
- W metodzie Ritza szukamy przybliżonej funkcji falowej jako kombinacji
liniowej funkcji
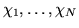 . W tym celu policzyliśmy macierze
. W tym celu policzyliśmy macierze
 i
i 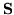 o elementach
o elementach
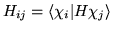 i
i
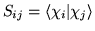 . Jeśli funkcje
. Jeśli funkcje 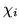 są
ortonormalne, macierz
są
ortonormalne, macierz 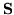 jest macierzą jednostkową; energia
stanu podstawowego otrzymana metodą Ritza jest wówczas równa
jest macierzą jednostkową; energia
stanu podstawowego otrzymana metodą Ritza jest wówczas równa
- a)
- wyznacznikowi macierzy
 ,
,
- b)
- sumie elementów diagonalnych
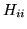 macierzy
macierzy  ,
,
- c)
- sumie wartości własnych macierzy
 ,
,
- d)
- najniższej wartości własnej macierzy
 .
.
Uwaga. W pytaniach dotyczących rachunku zaburzeń (5-8) zakładamy normalizację
pośrednią (
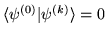 dla
dla 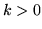 ) oraz
brak degeneracji.
) oraz
brak degeneracji.
- Poprawki
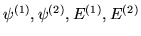 wiąże ze sobą
równanie
wiąże ze sobą
równanie
- a)
-
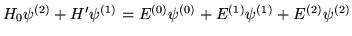
- b)
-
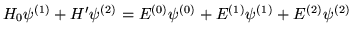
- c)
-
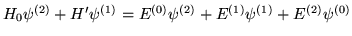
- d)
-
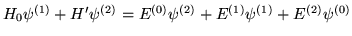
- Iloczyn skalarny
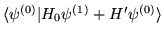 jest równy
jest równy
- Pierwsza poprawka do funkcji falowej dla
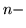 tego stanu,
tego stanu,
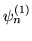 , dana jest wzorem
, dana jest wzorem
- Dokładna energia
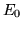 stanu podstawowego oraz współczynniki
stanu podstawowego oraz współczynniki
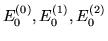 jej rozwinięcia w rachunku zaburzeń
spełniają zawsze warunek
jej rozwinięcia w rachunku zaburzeń
spełniają zawsze warunek
Edyta Malolepsza
2000-11-24
![\begin{displaymath}\begin{array}{l}
\psi_a(\alpha)=e^{-\alpha r},\\ \psi_b(\alp...
...\beta)=(1+\beta r)e^{-\alpha r^2},\makebox[3in]{}\\ \end{array}\end{displaymath}](img14.png)
 ,
,
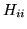 macierzy
macierzy  ,
,
 ,
,
 .
.