| a)
|
b)
|
| c)
|
d)
|
- a)
- gdy orbitale otrzymane w
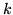 -tej iteracji są prawie takie same
jak orbitale
otrzymane w
-tej iteracji są prawie takie same
jak orbitale
otrzymane w 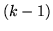 -szej iteracji,
-szej iteracji,
- b)
- gdy orbitale otrzymane w
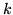 -tej iteracji są ortogonalne do orbitali
otrzymanych w
-tej iteracji są ortogonalne do orbitali
otrzymanych w 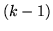 -szej iteracji,
-szej iteracji,
- c)
- gdy orbitale otrzymane w
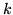 -tej iteracji są ortogonalne do siebie
nawzajem,
-tej iteracji są ortogonalne do siebie
nawzajem,
- d)
- gdy energie orbitalne otrzymane w
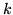 -tej iteracji są mniejsze niż
energie orbitalne otrzymane w
-tej iteracji są mniejsze niż
energie orbitalne otrzymane w 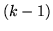 -szej iteracji.
-szej iteracji.
- a)
- są takie same jak orbitale jonu wodoropodobnego Ne
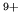 ,
,
- b)
- mają taką samą część kątową jak orbitale jonu Ne
 ,
ale inną część radialną,
,
ale inną część radialną,
- c)
- mają takie same wykładniki w funkcji
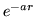 jak
orbitale jonu Ne
jak
orbitale jonu Ne , ale różnią się resztą części radialnej,
, ale różnią się resztą części radialnej,
- d)
- nie wykazują żadnego spośród ww. podobieństw do orbitali jonu
Ne
 .
.
| a) H | b) Be | c) C | d) N |
| a)
|
b)
|
| c) |
d) |
| a) 6-krotnie | b) 9-krotnie | c) 10-krotnie | d) 15-krotnie |
| a)
|
b)
|
c)
|
d)
|
| a) |
b) |
c) |
d) |