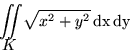Test matematyczny -- październik 1999
grupa Konrada Patkowskiego
- Iloczyn skalarny wektorów
![$[1,0,3]$](img1.png) i
i ![$[1,3,-3]$](img2.png) wynosi
wynosi
- Wartość wyrażenia
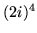 wynosi
wynosi
- Niech
Wyznacznik macierzy
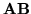 jest równy
jest równy
- Największa wartość funkcji
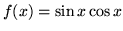 to
to
- Wartość wyrażenia
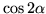 jest dla wszystkich
jest dla wszystkich 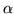 równa
równa
- Pochodną funkcji
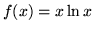 jest funkcja
jest funkcja
- Jeśli
to funkcja 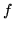 ma w punkcie
ma w punkcie 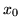
| a) maksimum |
b) minimum |
c) punkt siodłowy |
d) punkt przegięcia |
- Niech
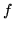 będzie funkcją różniczkowalną. Całka
będzie funkcją różniczkowalną. Całka
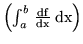 jest równa
jest równa
- Niech
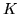 będzie kołem o środku w punkcie
będzie kołem o środku w punkcie 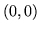 i promieniu 1.
Całka po zbiorze
i promieniu 1.
Całka po zbiorze 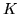
jest równa
- Rzuciliśmy zwykłą kostką do gry dwa razy -- wypadły dwie szóstki.
Prawdopodobieństwo, że w trzecim rzucie też wypadnie szóstka, jest równe
Edyta Malolepsza
2000-12-15
![\begin{displaymath}{\mathbf A}=\left[\begin{array}{ccc}1&0&0\\ 1&2&0\\ 1&2&3\\ \...
...[\begin{array}{ccc}
3&3&3\\ 0&2&2\\ 0&0&1\\ \end{array}\right].\end{displaymath}](img12.png)