Test matematyczny -- styczeń 2000 (III termin)
grupa Konrada Patkowskiego
- Pole kwadratu o przekątnej długości
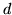 jest równe
jest równe
- Która z liczb podniesiona do kwadratu da w wyniku
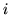 ?
?
- Liczba
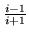 jest równa
jest równa
- Niech
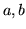 będą dowolnymi liczbami dodatnimi. Liczba
będą dowolnymi liczbami dodatnimi. Liczba 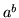 jest
równa
jest
równa
- Granica
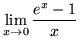 jest równa
jest równa
- Pochodną funkcji
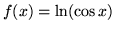 jest funkcja
jest funkcja
a) 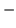 tg tg 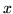 |
b) tg 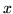 |
c) 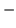 ctg ctg 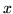 |
d) ctg 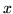 |
- Niech
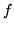 będzie funkcją liniową. Całka
będzie funkcją liniową. Całka
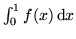 jest równa
jest równa
- Wskaż parę wektorów prostopadłych:
- Ile wynosi wyznacznik macierzy
![${\displaystyle
\left[\begin{array}{ccc} 1&i&0\\ 0&1&i\\ i&0&1\\ \end{array}\right]}$](img40.png) ?
?
- Jak nazywa się odcinek łączący pewne dwa punkty okręgu?
| a) styczna |
b) cięciwa |
c) wysokość |
d) promień |
Edyta Malolepsza
2000-12-15
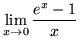 jest równa
jest równa
![${\displaystyle
\left[\begin{array}{ccc} 1&i&0\\ 0&1&i\\ i&0&1\\ \end{array}\right]}$](img40.png) ?
?