- Dla elektronu komutują następujące operatory:
a) 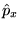 ,
, 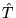 ,
b)
,
b) 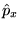 ,
, 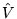 ,
c)
,
c) 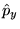 ,
, 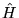 ,
d)
,
d) 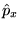 ,
, 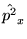 .
.
- Całkowalne z kwadratem są następujące funkcje :
a)
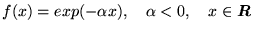
b)
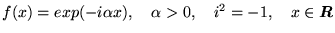
c)
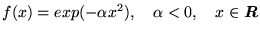
d)
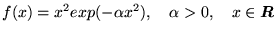 .
.
- Ortogonalne są funkcje :
a)
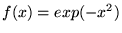 oraz
oraz
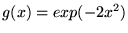 ,
,
b)
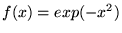 oraz
oraz
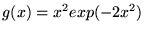 ,
,
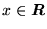
c)
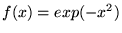 oraz
oraz
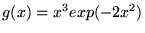 ,
,
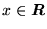
d)
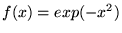 oraz
oraz
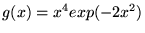 ,
,
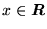 .
.
- Niech
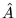 oznacza operator hermitowski. Niech
oznacza operator hermitowski. Niech 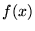 jest funkcją własną operatora
jest funkcją własną operatora 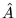 , zaś
, zaś 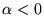 jest odpowiadającą wartością własną. Czy
wartością własną operatora
jest odpowiadającą wartością własną. Czy
wartością własną operatora
 (kwadrat operatora
(kwadrat operatora 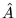 ) jest :
) jest :
a) 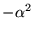 ; b)
; b) 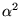 ;
c) 0 ; d)
;
c) 0 ; d) 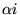 , gdzie
, gdzie 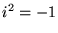 .
.
- 5-krotna degeneracja wartości własnej
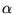 operatora
operatora
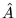 oznacza, że :
oznacza, że :
a) jednej funkcji własnej 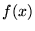 odpowiada 5 różnych wartości
zespolonych
odpowiada 5 różnych wartości
zespolonych 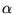 , które mają jednakowy moduł
, które mają jednakowy moduł
b) istnieje 5 liniowo niezależnych funkcji własnych , z których
każda odpowiada wartości własnej 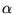
c) istnieje 5 liniowo zależnych funkcji własnych , z których
każda odpowiada wartości własnej 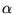
d) istnieje 5 liniowo niezależnych funkcji własnych,
które nie są całkowalne z kwadratem.
- Wartosc srednia hamiltonianu, t.j. liczba
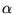 =<
=<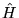 >,
może być liczbą o własności :
>,
może być liczbą o własności :
a) istnieje 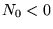 takie, że dla każdego
takie, że dla każdego 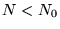 zachodzi
zachodzi 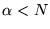 .
.
b) istnieje taka liczba zespolona 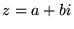 , że
, że 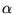 =
= 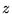 dla
dla 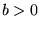
c) istnieje taka liczba zespolona 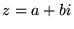 , że
, że 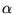 =
= 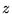 dla
dla 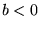
d) istnieje taka liczba zespolona 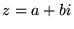 , że
, że 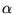 =
= 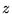 dla
dla 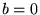 .
.
- Pewna cząstka może przebywać wyłącznie na osi X
w ograniczonym obszarze o współrzędnych
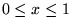 .
Zmiana w czasie jej funkcji falowej
.
Zmiana w czasie jej funkcji falowej 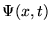 jest określona równaniem
Czy funkcją
jest określona równaniem
Czy funkcją 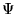 może być (zastosowano jednostki atomowe,
może być (zastosowano jednostki atomowe, 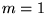 ,
oraz
,
oraz
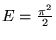 )
)
a)
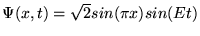
b)
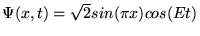
c)
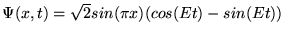
d)
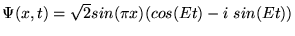 ,
gdzie
,
gdzie 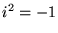 .
.
- Pewna cząstka może przebywać wyłącznie na osi X
w ograniczonym obszarze o współrzędnych
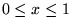 .
Przedział ten dzielimy na trzy równe podprzedziały :
.
Przedział ten dzielimy na trzy równe podprzedziały :
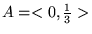 ,
,
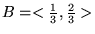 ,
,
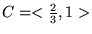 . Cząstka ma funkcję falową
. Cząstka ma funkcję falową
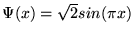 .
.
Niech 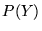 oznacza prawdopodobieństwo znalezienia tej cząstki
w przedziale
oznacza prawdopodobieństwo znalezienia tej cząstki
w przedziale 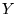 , gdzie
, gdzie 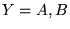 lub
lub 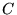 . Czy prawdą jest, że :
. Czy prawdą jest, że :
a)
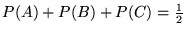 b)
b) 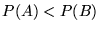 c)
c) 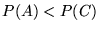 d)
d) 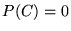 .
.
- Niech
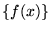 jest zbiorem funkcji ciągłych,
różniczkowalnych i całkowalnych z kwadratem dla
jest zbiorem funkcji ciągłych,
różniczkowalnych i całkowalnych z kwadratem dla
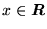 .
Czy liniowy jest operator określony następująco :
.
Czy liniowy jest operator określony następująco :
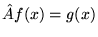 , gdzie
, gdzie 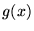 ma postać :
ma postać :
a)
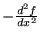 , b)
, b)
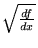 ,
c) (
,
c) (
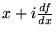 ) (
) (
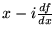 ) ,
d)
) ,
d) 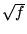 .
.
- Niech dla operatora hermitowskiego
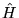 zachodzi :
zachodzi :
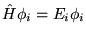 , dla
, dla 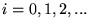 . Niech
. Niech
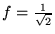 (
(
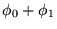 ) . Wartość średnia
) . Wartość średnia
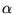 =<
=<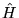 > tego
operatora obliczona z funkcją f jest równa :
> tego
operatora obliczona z funkcją f jest równa :
a) 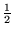 (
( 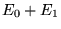 )
b)
)
b) 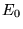 c)
c) 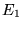 d)
d) 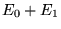 .
.
Edyta Malolepsza
2000-11-28