(
Który z podanych zestawów energii przedstawia sumę energii oscylatora
harmonicznego i poprawki pierwszego rzędu według rachunku zaburzeń :
a)
![]() = 0.575,
= 0.575,
![]() = 1.875,
= 1.875,
![]()
b)
![]() = 0.425,
= 0.425,
![]() = 1.125,
= 1.125,
![]()
c)
![]() = 0.575,
= 0.575,
![]() = 1.125,
= 1.125,
![]()
d)
![]() = 0.575,
= 0.575,
![]() = 1.875,
= 1.875,
![]()
gdzie
a)
a)
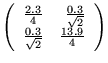 b)
b)
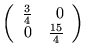 c)
c)
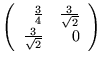 d)
d)
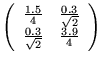
Załóżmy ponadto, że hamiltonian atomu wodoru, w jednostkach atomowych,
ma postać :
Gdy obliczymy wartość średnią operatorów
Wykorzystując następnie metodę wariacyjną otrzymamy energię
a)
Jakie jest prawidłowe wyrażenie na
a)
c)
a)
c)
a)
b)
c)
d)
Czy prawdziwe jest objaśnienie tego ciekawego fenomenu :
a) istnieją wyjątki od zasady wariacyjnej i tu mamy przykład
b) funkcja próbna powinna znikać na krańcach przedziału, tj.
c) funkcja próbna nie musi znikać na krańcach przedziału, ale powinna być całkowalna z kwadratem na odcinku
d) wybrano niewłaściwą funkcję próbną, gdyż nie jest ona dwukrotnie różniczkowalna, a więc nieprawidłowo obliczono wartość średnią hamiltonianu.