- Załóżmy, że mamy cztery trójelektronowe funkcje falowe podane
niżej. Która z nich spełnia wymagania tzw. zakazu Pauliego :
a)
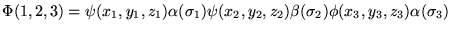
b)
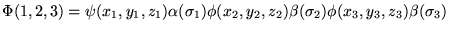
c)
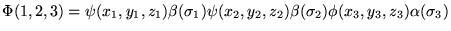
d)
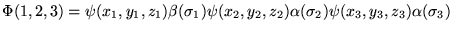
gdzie 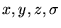 - wspólrzedne elektronów, zaś
- wspólrzedne elektronów, zaś 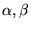 - funkcje spinowe.
- funkcje spinowe.
- Niech dana będzie następująca funkcja dwóch zmiennych
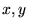 :
:
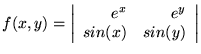 =
=
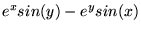
Obliczamy następujące całki oznaczone (zakładamy, że
ich wartości są skończone) :
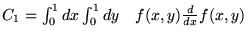
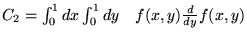
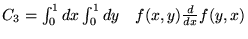
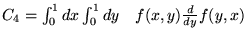
Czy prawdziwe są równości (można je sprawdzić bez jawnego obliczenia
całek podwójnych) :
a) 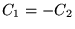 b)
b) 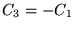 c)
c) 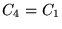 d)
d) 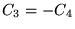
- Niech dana będzie następująca funkcja czterech zmiennych
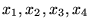 :
:
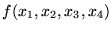 =
=
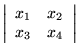 =
=
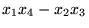
Obliczamy następujące całki oznaczone (zakładamy, że są skończone) :
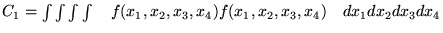
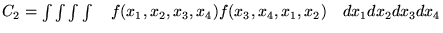
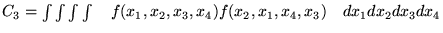
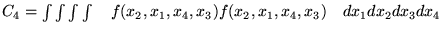
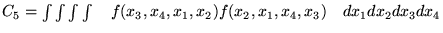
Czy prawdziwe są równości :
a) 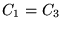 b)
b) 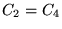 c)
c) 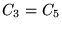 d)
d) 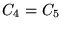
- Załóżmy, że podział hamiltonianu
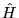 na część
niezaburzoną
na część
niezaburzoną 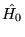 oraz zaburzenie
oraz zaburzenie 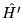 jest następujący:
jest następujący:
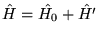 , przy czym znamy wszystkie funkcje własne
, przy czym znamy wszystkie funkcje własne
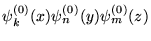 i
wartości własne
i
wartości własne
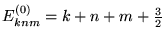 hamiltonianu
hamiltonianu
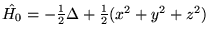 .
Jak widać, jest to zaburzony trójwymiarowy oscylator harmoniczny, gdzie
liczby
.
Jak widać, jest to zaburzony trójwymiarowy oscylator harmoniczny, gdzie
liczby 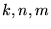 przyjmują wartości ze zioru
przyjmują wartości ze zioru
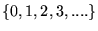 .
Jeżeli operator
.
Jeżeli operator 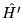 jest niezerowy, to niektóre poziomy energetyczne
oscylatora harmonicznego mogą ulec rozszczepieniu.
Jeżeli wybierzemy
jest niezerowy, to niektóre poziomy energetyczne
oscylatora harmonicznego mogą ulec rozszczepieniu.
Jeżeli wybierzemy
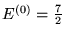 (jednostki atomowe),
to liczba poziomów po rozszczepieniu wynosić może :
(jednostki atomowe),
to liczba poziomów po rozszczepieniu wynosić może :
a) nie więcej, niż 6 b) ponad 12
c) ponad 6, ale mniej niż 12 
d) 1, tzn. nie rozszczepi się, ponieważ poziom ten nie jest zdegenerowany
- Aby można było zinterpretować elektronowe widmo absorpcyjne
jonu
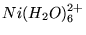 w hydracie siarczanu niklu
w hydracie siarczanu niklu
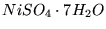 zakłada się, że przejścia elektronowe zachodzą pomiędzy
poziomami
zakłada się, że przejścia elektronowe zachodzą pomiędzy
poziomami 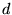 niklu, rozszczepionymi pod wpływem pola elektrycznego
cząsteczek wody. Zakłada się również, że w jonie
niklu, rozszczepionymi pod wpływem pola elektrycznego
cząsteczek wody. Zakłada się również, że w jonie 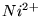 (bez pola ligandów) 8 elektronów opisać można przy pomocy orbitali
(bez pola ligandów) 8 elektronów opisać można przy pomocy orbitali 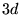 .
Liczba rozszczepionych poziomów
.
Liczba rozszczepionych poziomów 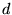 jonu
jonu 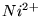 pod wpływem ligandów
wynosi :
pod wpływem ligandów
wynosi :
a) dokładnie 8
b) więcej, niż 6
c) mniej, niż 6
d) dokładnie 6, tzn. tyle, ile wynosi liczba cząsteczek wody.
- Operatory spinowe spełniają następujące relacje
(w jednostkach atomowych) :
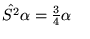
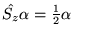
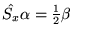
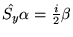
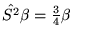
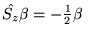
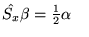
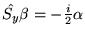
Ponadto, spełnione są relacje komutacyjne :
![$ \left[ \hat{ S_x},\hat{S_y} \right] = i \hat{S_z}, \quad $](img55.png)
![$ \left[ \hat{ S_y},\hat{S_z} \right] = i \hat{S_x}, \quad $](img56.png)
![$ \left[ \hat{ S_z},\hat{S_x} \right] = i \hat{S_y}, \quad $](img57.png) ,
gdzie
,
gdzie 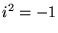
Czy prawidłowe są wyniki działania sum iloczynów operatorów na
funkcje spinowe :
a)
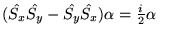 b)
b)
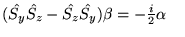 c)
c)
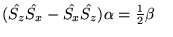 d)
d)
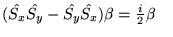
- Dla atomu helu
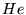 w stanie podstawowym wybieramy funkcję
próbną
w stanie podstawowym wybieramy funkcję
próbną 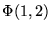
(1,2-numerują współrzędne elektronów) :
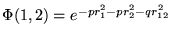
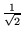 (
(
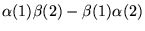 ) ,
) ,
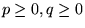 ,
,
gdzie :
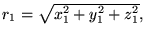
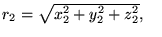 są
odległościami elektron-jądro,
zaś
są
odległościami elektron-jądro,
zaś
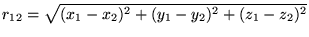 oznacza
odległość międzyelektronową.
oznacza
odległość międzyelektronową.
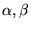 są funkcjami spinowymi. Czy prawdziwe są zdania:
są funkcjami spinowymi. Czy prawdziwe są zdania:
a)
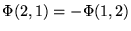 tylko wtedy, gdy
tylko wtedy, gdy 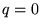
b) postać 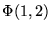 odpowiada tzw. przybliżeniu jednoelektronowemu
do funkcji falowej dwuelektronowej tylko wtedy, gdy
odpowiada tzw. przybliżeniu jednoelektronowemu
do funkcji falowej dwuelektronowej tylko wtedy, gdy 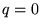
c) postać 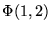 odpowiada tzw. przybliżeniu jednoelektronowemu
do funkcji falowej dwuelektronowej tylko wtedy, gdy
odpowiada tzw. przybliżeniu jednoelektronowemu
do funkcji falowej dwuelektronowej tylko wtedy, gdy 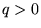
d)
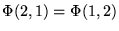 , jeżeli
, jeżeli 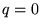
- Załóżmy, że operator rzutu spinu
całkowitego na oś
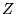 ma postać sumy operatorów jednoelektronowych :
ma postać sumy operatorów jednoelektronowych :
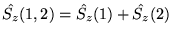 .
Załóżmy również, że mamy dwie różne funkcje spinowe dwuelektronowe:
.
Załóżmy również, że mamy dwie różne funkcje spinowe dwuelektronowe:
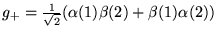
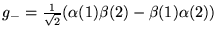
Prawidłowy wynik działania operatora
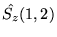 na te funkcje jest następujący :
na te funkcje jest następujący :
a)
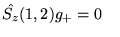 b)
b)
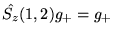 c)
c)
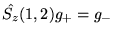 d)
d)
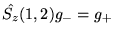
Edyta Malolepsza
2000-11-28
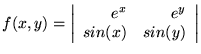 =
=
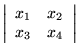 =
=