- Funkcja falowa (nieznormalizowana) cząstki
swobodnej poruszającej się wzdłuż osi x ma postać
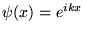 . Pęd cząstki opisanej tą funkcją równy jest:
. Pęd cząstki opisanej tą funkcją równy jest:
a) 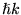 ,
b)
,
b) 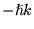 ,
c)
,
c) 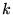 ,
d)
,
d) 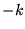 .
.
- Warunki, jak w zad. 1. Które z poniższych
stwierdzeń jest nieprawdziwe:
a) cząstce odpowiada fala o długości
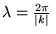 ,
b) funkcja
,
b) funkcja 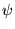 nie daje się znormalizować w przedziale
nie daje się znormalizować w przedziale
![$[-\infty, \infty] $](img8.png) ,
c) funkcja falowa
,
c) funkcja falowa 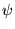 przedstawia falę stojącą,
d) gdy
przedstawia falę stojącą,
d) gdy 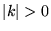 , energia własna
, energia własna 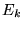 jest dwukrotnie
zdegenerowana.
jest dwukrotnie
zdegenerowana.
- Cząstka o masie
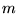 porusza się w
jednowymiarowym pudle potencjału o długości
porusza się w
jednowymiarowym pudle potencjału o długości 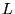 . Które z poniższych stwierdzeń jest nieprawdziwe:
. Które z poniższych stwierdzeń jest nieprawdziwe:
a) energia cząstki jest zawsze 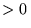 ,
b) funkcja falowa cząstki znika poza obszarem pudła,
c) poziomy energetyczne cząstki są niezdegenerowane,
,
b) funkcja falowa cząstki znika poza obszarem pudła,
c) poziomy energetyczne cząstki są niezdegenerowane,
d) poziomy energetyczne cząstki są równo oddalone od siebie.
- Warunki, jak w zad. 3. Gdy rozmiary pudła
zmniejszyć 2 razy, to różnica energii dwóch sąsiednich poziomów energetycznych cząstki
a) zwiększy się 2 razy,
b) zmniejszy się 2 razy,
c) zwiększy się 4 razy,
d) zmniejszy się 4 razy.
- Warunki, jak w zad. 3. Gdy masa cząstki zostanie
zwiększona 2 razy, to różnica energii dwóch sąsiednich poziomów energetycznych cząstki
a) zwiększy się 2 razy,
b) zmniejszy się 2 razy,
c) zwiększy się 4 razy,
d) zmniejszy się 4 razy.
- Bariera potencjału: cząstka porusza się
w obszarze I
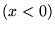 w potencjale
w potencjale 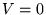 , w obszarze II
, w obszarze II
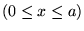 w potencjale
w potencjale 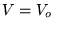
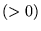 , i w obszarze III
, i w obszarze III
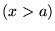 w potencjale
w potencjale 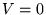 . Jeśli energia cząstki
. Jeśli energia cząstki 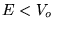 , to długości fali
, to długości fali 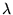 odpowiadające cząstce w obszarach I, II i III spełniają zależności:
odpowiadające cząstce w obszarach I, II i III spełniają zależności:
a)
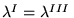 ,
, 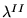 jest
niezdefiniowana,
b)
jest
niezdefiniowana,
b)
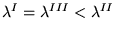 ,
,
c)
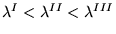 ,
d)
,
d)
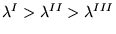 .
.
- Warunki, jak w zadaniu 6. Jeśli energia
cząstki
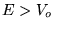 , to:
, to:
a)
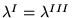 ,
, 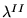 jest
niezdefiniowana,
b)
jest
niezdefiniowana,
b)
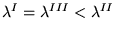 ,
,
c)
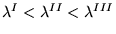 ,
d)
,
d)
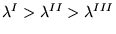 .
.
- Warunki jak w zad. 6. Efekt tunelowy polega na
przechodzeniu cząstki przez barierę, gdy:
a) 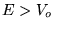 ,
b)
,
b) 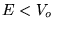 ,
c)
,
c) 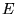 jest dowolne,
d)
jest dowolne,
d) 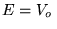 .
.
Edyta Malolepsza
2000-11-22
![]() ,
b)
,
b) ![]() ,
c)
,
c) ![]() ,
d)
,
d) ![]() .
.