- W rachunku zaburzeń Rayleigha-Schrödingera
(RS) przedstawiamy hamiltonian układu w postaci
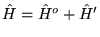 , a funkcje i wartości własne
, a funkcje i wartości własne 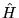 i
i 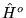 oznaczamy, odpowiednio, przez
oznaczamy, odpowiednio, przez 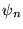 i
i 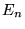 , oraz
, oraz
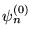 i
i 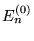 (
(
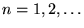 ). Który z poniższych warunków nie jest prawdziwy w rachunku zaburzeń RS?
). Który z poniższych warunków nie jest prawdziwy w rachunku zaburzeń RS?
a)
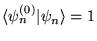 ,
b)
,
b)
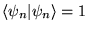 ,
c)
,
c)
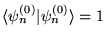 ,
,
d) Znamy rozwiązania równania
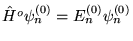 .
.
-
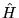 jest hamiltonianem układu,
jest hamiltonianem układu, 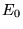 jego najmniejszą wartością własną, a
jego najmniejszą wartością własną, a 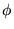 jest pewną funkcją falową. Zasada wariacyjna jest równoważna stwierdzeniu,
że:
jest pewną funkcją falową. Zasada wariacyjna jest równoważna stwierdzeniu,
że:
a)
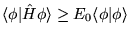 ,
b)
,
b)
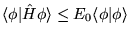 ,
c)
,
c)
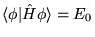 , jeśli
, jeśli
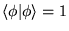 ,
d)
,
d)
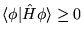 , jeśli
, jeśli
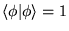 .
.
- Oznaczenia jak w zad. 2. Funkcja
próbna
![$\phi[c]$](img20.png) zależy od rzeczywistego parametru
zależy od rzeczywistego parametru 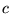 . Metoda wariacyjna polega na:
. Metoda wariacyjna polega na:
a) znalezieniu optymalnej wartości 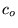 , takiej, że
, takiej, że
![$\hat{H}
\phi[c_o] = E_0 \phi[c_o]$](img23.png) ,
,
b) obliczeniu wartości
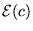 ,
,
c) znalezieniu optymalnej wartości 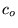 , takiej, że
, takiej, że
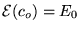 ,
,
d) znalezieniu optymalnej wartości 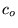 , takiej, że
, takiej, że
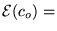 minimum,
minimum,
gdzie
![$\mathcal{E}(c) = \frac{\langle \phi[c] \vert \hat{H} \phi[c]
\rangle}{ \langle \phi[c] \vert \phi[c] \rangle}$](img27.png)
- Która z poniższych funkcji próbnych
![$\phi[c]$](img20.png) da najlepszy
wynik w metodzie wariacyjnej zastosowanej do opisu atomu wodoru:
da najlepszy
wynik w metodzie wariacyjnej zastosowanej do opisu atomu wodoru:
a) 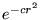 , b)
, b) 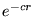 , c)
, c) 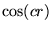 , d)
, d)
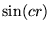 ,
,
gdzie 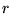 jest współrzędną radialną położenia elektronu (
jest współrzędną radialną położenia elektronu (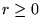 ).
).
- Oznaczenia jak w zad. 1. Przedstawienie:
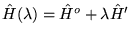 , gdzie
, gdzie
![$\lambda \in [0,1]$](img35.png) , służy:
, służy:
a) znalezieniu takiego 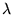 , że potrafimy rozwiązać równanie
, że potrafimy rozwiązać równanie
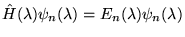 ,
,
b) rozwinięciu
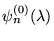 i
i
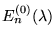 w
szeregi Taylora w otoczeniu
w
szeregi Taylora w otoczeniu 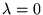 ,
,
c) przejściu do granicy
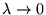 w celu znalezienia
poprawek do energii,
w celu znalezienia
poprawek do energii,
d) znalezieniu takiego 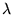 , by operator
, by operator
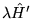 był
mały.
był
mały.
- Oznaczenia jak w zad. 1. Które z poniższych
stwierdzeń jest nieprawdziwe?
a)
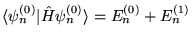 , b) Do wyznaczenia
, b) Do wyznaczenia 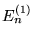 wystarczy znajomość
wystarczy znajomość 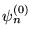 , c)
, c) 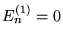 , jeli
, jeli
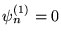 , d)
, d)
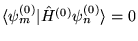 dla
dla 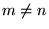 .
.
- Oznaczenia jak w zad. 1. Które z poniższych
stwierdzeń jest nieprawdziwe?
a)
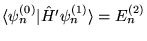 ,
b)
,
b) 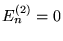 , jeli
, jeli
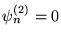 ,
,
c)
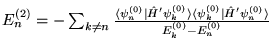 ,
,
d)
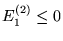 , jeli
, jeli
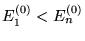 dla
dla 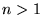 .
.
- Oznaczenia jak w zad. 2 i 3. Równanie
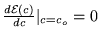 określa:
określa:
a) warunek konieczny, by ![$\phi[c_o]$](img57.png) była funkcją własną
była funkcją własną
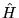 ,
,
b) warunek wystarczajcy, by
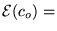 minimum,
minimum,
c) warunek konieczny, by ![$\phi[c_o]$](img57.png) dała się znormalizować.
dała się znormalizować.
d) warunek konieczny, by
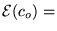 minimum.
minimum.
Edyta Malolepsza
2000-12-20