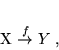Mówi się, że zostało określone odwzorowanie 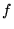 zbioru
zbioru 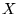 w zbiór
w zbiór 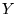 , jeśli każdemu elementowi
, jeśli każdemu elementowi 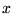 zbioru
zbioru 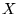 został przyporządkowany jeden element
został przyporządkowany jeden element 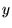 ze zbioru
ze zbioru 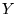 . Dany element
. Dany element 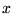 zbioru
zbioru 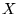 nazywamy argumentem odworowania
nazywamy argumentem odworowania 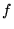 , a przyporządkowany mu element
, a przyporządkowany mu element 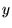 zbioru
zbioru 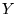 nazywamy wartością odwzorowania
nazywamy wartością odwzorowania 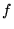 odpowiadającą
odpowiadającą 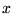 , co zapisujemy w postaci
, co zapisujemy w postaci 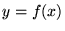 .
Zbiór
.
Zbiór 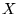 nazywamy dziedziną odwzorowania
nazywamy dziedziną odwzorowania 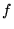 , a zbiór
, a zbiór 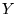 przeciwdziedziną tego odwzorowania.
Odwzorowanie jest określone jednoznacznie przez swoją dziedzinę i przeciwdziedzinę, oraz przez
podanie zależności
przeciwdziedziną tego odwzorowania.
Odwzorowanie jest określone jednoznacznie przez swoją dziedzinę i przeciwdziedzinę, oraz przez
podanie zależności 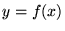 . Odwzorowanie zapisuje się symbolicznie w postaci ''strzałki'':
. Odwzorowanie zapisuje się symbolicznie w postaci ''strzałki'':
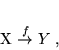 |
(70) |
inna forma to 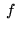 :
:
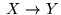 .
Podana wyżej definicją odwzorowania, wykorzystująca bardziej rozbudowaną notację matematyczną, wygląda następująco:
.
Podana wyżej definicją odwzorowania, wykorzystująca bardziej rozbudowaną notację matematyczną, wygląda następująco:
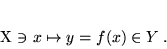 |
(71) |
gdzie zakłada sie, że
(i) każdemu 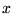 jest przypisane pewne
jest przypisane pewne 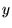 ,
,
(ii) jeśli danemu 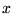 są przypisane
są przypisane 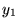 i
i 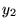 , to
, to 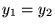 .
.
Dwa odwzorowania 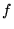 i
i 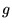 są identyczne, co zapisuje się jako
są identyczne, co zapisuje się jako 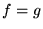 , wtedy i tylko wtedy gdy:
, wtedy i tylko wtedy gdy:
(i) dziedziny 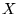 obu odwzorowań są identyczne,
obu odwzorowań są identyczne,
(ii) przeciwdziedziny 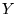 obu odwzorowań są identyczne,
obu odwzorowań są identyczne,
(iii) dla każdego 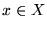 zachodzi
zachodzi 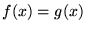 .
.
Gdy zbiory 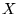 i
i 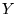 są zbiorami liczb (podzbiorami R lub C), to odwzorowanie
są zbiorami liczb (podzbiorami R lub C), to odwzorowanie 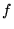 nazywa się funkcją. Przykład: poniższe definicje określają trzy różne funkcje:
nazywa się funkcją. Przykład: poniższe definicje określają trzy różne funkcje:
(a) 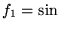 , o dziedzinie R i przeciwdziedzinie R,
, o dziedzinie R i przeciwdziedzinie R,
(b) 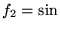 , o dziedzinie R i przeciwdziedzinie
, o dziedzinie R i przeciwdziedzinie ![$[-1, 1]$](img195.png) ,
,
(c) 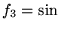 , o dziedzinie
, o dziedzinie ![$[0,2\pi]$](img197.png) i przeciwdziedzinie
i przeciwdziedzinie ![$[-1, 1]$](img195.png) .
.
UWAGA: z powyższych rozważań wynika, że powinno się rozróżniać symbol 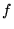 , określający odwzorowanie, od symbolu
, określający odwzorowanie, od symbolu 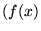 , określającego wartość owzorowania
, określającego wartość owzorowania 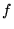 odpowiadającą danemu argumentowi
odpowiadającą danemu argumentowi 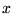 . Zapisu
. Zapisu 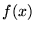 na określenie odwzorowania stosuje się czasem, by podkreślić, jak wygląda zbiór argumentów odwzorowania: np.
na określenie odwzorowania stosuje się czasem, by podkreślić, jak wygląda zbiór argumentów odwzorowania: np. 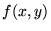 jako symbol odwzorowania wskazuje, że zbiorem argumentów jest zbiór par elementów
jako symbol odwzorowania wskazuje, że zbiorem argumentów jest zbiór par elementów 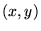 .
.
- Jeśli
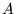 jest podzbiorem dziedziny odwzorowania
jest podzbiorem dziedziny odwzorowania 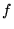 ,
, 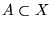 , to przez
, to przez 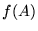 oznacza się podzbiór przeciwdziedziny Y, złożony ze wszystkich
oznacza się podzbiór przeciwdziedziny Y, złożony ze wszystkich 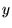 takich, że istnieje
takich, że istnieje 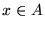 taki, że
taki, że 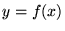 . Zbiór
. Zbiór 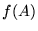 nazywa się obrazem zbioru
nazywa się obrazem zbioru 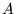 w odwzorowaniu
w odwzorowaniu 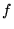 . Zbiór
. Zbiór 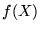 , gdzie
, gdzie 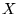 jest dziedziną odwzorowania
jest dziedziną odwzorowania 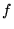 , nazywa się po prostu obrazem odwzorowania
, nazywa się po prostu obrazem odwzorowania 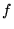 . Oczywiście
. Oczywiście 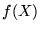 jest podzbiorem przeciwdziedziny
jest podzbiorem przeciwdziedziny 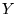 ,
,
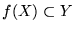 , ale niekoniecznie równa się
, ale niekoniecznie równa się 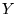 .
.
Edyta Malolepsza
2000-12-20