- Macierz kwadratowa
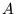 jest hermitowska, jeśli jej
elementy spełniają warunek:
jest hermitowska, jeśli jej
elementy spełniają warunek:
a)
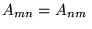 ,
b)
,
b)
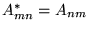 ,
c)
,
c)
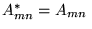 ,
d)
,
d)
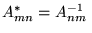 .
.
-
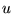 ,
, 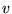 i
i 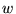 są dowolnymi
wektorami w zespolonej przestrzeni wektorowej, a
są dowolnymi
wektorami w zespolonej przestrzeni wektorowej, a 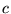 jest dowolną liczbą zespoloną. Iloczyn skalarny nie spełnia warun
ku :
jest dowolną liczbą zespoloną. Iloczyn skalarny nie spełnia warun
ku :
a)
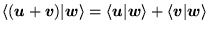 ,
b)
,
b)
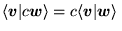 ,
c)
,
c)
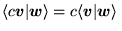 ,
d)
,
d)
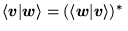 .
.
- Założenia jak w zad. (2). Jeśli
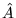 jest operatorem liniowym w zespolonej przestrzeni wektorowej, to która równość jest fałszywa?
jest operatorem liniowym w zespolonej przestrzeni wektorowej, to która równość jest fałszywa?
a)
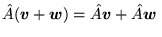 ,
b)
,
b)
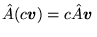 ,
c)
,
c)
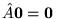 ,
d)
,
d)
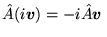 ,
,
gdzie 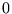 jest wektorem zerowym.
jest wektorem zerowym.
- Warunek, że operator
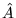 jest hermitowski, zapisać
można jako:
jest hermitowski, zapisać
można jako:
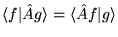 , dla dowolnych funkcji falowych
, dla dowolnych funkcji falowych 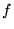 i
i 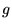 .
.
Dla funkcji jednej zmiennej warunek ten przyjmuje postać:
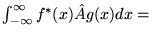
a)
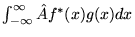 ,
b)
,
b)
![$ \int_{-\infty}^{\infty} [\hat{A} f^*(x)] g(x) dx$](img25.png) ,
c)
,
c)
![$ \int_{-\infty}^{\infty} [\hat{A} f(x)]^* g(x) dx$](img26.png) ,
,
d)
![$ \int_{-\infty}^{\infty} [\hat{A} f(x)] g(x)^* dx$](img27.png) .
.
- Który z poniższych operatorów liniowych, działających na
funkcje zmiennej
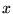 , nie jest operatorem hermitowskim?
, nie jest operatorem hermitowskim?
a)
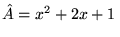 ,
b)
,
b)
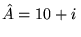 ,
c)
,
c)
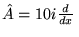 ,
d)
,
d)
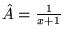 .
.
- Macierze
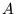 ,
, 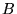 i
i 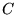 mają wymiary, odpowiednio,
mają wymiary, odpowiednio,
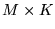 ,
, 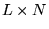 i
i 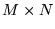 . Jeśli
. Jeśli
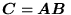 , to musi zachodzić (wskaż stwierdzenie f
ałszywe):
, to musi zachodzić (wskaż stwierdzenie f
ałszywe):
a) 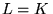 ,
b)
,
b)
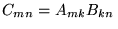 ,
c) jeśli
,
c) jeśli
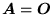 , to
, to
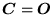 ,
,
d) jeśli
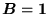 , to
, to
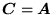 ,
,
gdzie 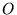 jest macierzą zerową, a
jest macierzą zerową, a 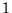 jest macierzą
jednostkową odpowiednich wymiarów.
jest macierzą
jednostkową odpowiednich wymiarów.
- Niech
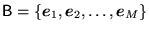 i
i
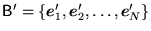 będą
dwoma bazami pewnej zespolonej przestrzeni wektorowej. Musi zachodzić (wskaż stwierdzenie fałszywe):
będą
dwoma bazami pewnej zespolonej przestrzeni wektorowej. Musi zachodzić (wskaż stwierdzenie fałszywe):
a) 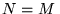 ,
b)
,
b) 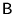 i
i 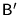 są zbiorami wektorów liniowo
niezależnych,
są zbiorami wektorów liniowo
niezależnych,
c) jesli macierz 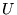 definiuje transformację bazy
definiuje transformację bazy 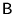 w
w
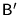 , to
, to
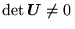 ,
d) żaden wektor bazy
,
d) żaden wektor bazy 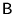 nie może być kombinacją liniową
wektorów bazy
nie może być kombinacją liniową
wektorów bazy 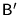 (i na odwrót).
(i na odwrót).
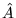 jest operatorem hermitowskim. Które z poniższych
stwierdzeń jest fałszywe:
jest operatorem hermitowskim. Które z poniższych
stwierdzeń jest fałszywe:
a) funkcja własna 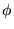 operatora
operatora 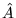 spełnia warunek
spełnia warunek
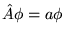 , gdzie
, gdzie 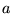 jest odpowiednią wartością własną,
jest odpowiednią wartością własną,
b) wartości własne 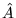 mogą być liczbami ujemnymi,
mogą być liczbami ujemnymi,
c) funkcje własne 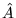 odpowiadające różnym wartościom
wlasnym są ortogonalne,
odpowiadające różnym wartościom
wlasnym są ortogonalne,
d) wartości własne 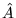 mogą być liczbami zespolonymi,
mogą być liczbami zespolonymi,
Edyta Malolepsza
2000-11-24