- Wymiar stałej Plancka h to:
a) długość 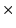 czas,
b) energia,
c) energia
czas,
b) energia,
c) energia 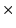 czas,
d) długość.
czas,
d) długość.
- Układ fizyczny opisany jest przy pomocy
hamiltonianu
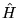 , któremu odpowiadają funkcje własne
, któremu odpowiadają funkcje własne 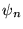 i wartości własne
i wartości własne 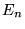 (
(
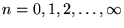 ). Ukł
ad jest w stanie opisanym funkcją falową (znormalizowaną)
). Ukł
ad jest w stanie opisanym funkcją falową (znormalizowaną)
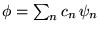 , gdzie więcej niż jedna wartość
, gdzie więcej niż jedna wartość 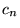 jest różna od zera.. Pojedynczy pomiar energii w tym stanie da j
ako wynik:
jest różna od zera.. Pojedynczy pomiar energii w tym stanie da j
ako wynik:
a) najniższą wartość 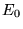 ,
b) jedną z wartości
,
b) jedną z wartości 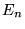 , z prawdopodobieństwem
, z prawdopodobieństwem 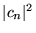 ,
c) wartość
,
c) wartość
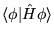 ,
d) wartość nieokreśloną, bo
,
d) wartość nieokreśloną, bo 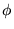 nie jest funkcją własną
nie jest funkcją własną
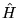 .
.
- By
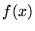 mogła być funkcją falową musi być spełnione
(wskaż warunek nieistotny):
mogła być funkcją falową musi być spełnione
(wskaż warunek nieistotny):
a) 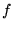 jest ciągła,
b)
jest ciągła,
b)
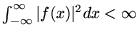 ,
c)
,
c) 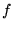 jest różniczkowalna,
jest różniczkowalna,
d) 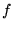 jest rzeczywista.
jest rzeczywista.
- Jeśli cząstka opisana jest niezależną od czasu funkcją
falową
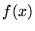 , to gęstość prawdopodobieństwa znalezienia cząstki w punkcie
, to gęstość prawdopodobieństwa znalezienia cząstki w punkcie 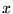 wyraża się przez:
wyraża się przez:
a) 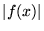 ,
b)
,
b)
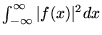 ,
c)
,
c) 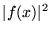 ,
d)
,
d) 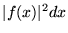 .
.
- Jeśli operatory hermitowskie
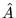 i
i 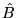 są
przemienne, to:
są
przemienne, to:
a) mają te same wartości własne,
b) są do siebie proporcjonalne,
c) odpowiadające im zmienne dynamiczne spełniają zasadę
nieoznaczoności,
d) można znaleźć wspólny układ funkcji własnych tych
operatorów.
- Jeśli cząstka opisana jest zależną od czasu funkcją
falową
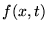 , to warunek normalizacji tej funkcji ma postać:
, to warunek normalizacji tej funkcji ma postać:
a)
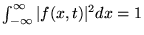 (dla każdej
wartości
(dla każdej
wartości 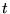 ),
b)
),
b)
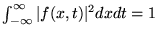 ,
,
c)
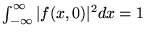 ,
d)
,
d)
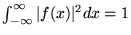 .
.
- Który z poniższych warunków nie charakteryzuje
stanu stacjonarnego układu kwantowego, złożonego z jednej cząstki poruszającej się wzdłuż osi
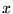 :
:
a) gęstość prawdopodobieństwa znalezienia cząstki w danym
punkcie 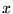 nie zależy od czasu,
b) cząstka spoczywa (pomiar położenia daje zawsze tę samą
wartość)
c) niezależna od czasu funkcja falowa stanu cząstki jest jedną z
funkcji własnych hamiltonianu,
d) energia cząstki jest ściśle określona (pomiar daje zawsze tę
samą wartość).
nie zależy od czasu,
b) cząstka spoczywa (pomiar położenia daje zawsze tę samą
wartość)
c) niezależna od czasu funkcja falowa stanu cząstki jest jedną z
funkcji własnych hamiltonianu,
d) energia cząstki jest ściśle określona (pomiar daje zawsze tę
samą wartość).
- średnia z
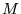 pomiarów energii (
pomiarów energii (
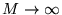 )
układu opisanego w zad. 2 wyniesie:
)
układu opisanego w zad. 2 wyniesie:
a)
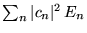 ,
b)
,
b)
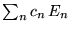 ,
c)
,
c)
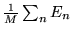 ,
d)
,
d) 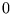 .
.
Edyta Malolepsza
2000-11-23