Liczby zespolone
Zbiór liczb rzeczywistych oznaczamy przez 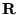 , a zbiór liczb zespolonych przez
, a zbiór liczb zespolonych przez 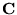 . Liczba zespolona
. Liczba zespolona 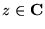 może być zapisana w postaci
może być zapisana w postaci
 |
(1) |
a 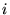 jest tzw. jednostką urojoną, spełniającą warunek
jest tzw. jednostką urojoną, spełniającą warunek
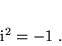 |
(2) |
Potocznie zapisuje się: 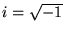 .
.
- Dla każdej liczby zespolonej
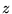 danej w postaci (1) definiuje się liczbę zespoloną sprzężoną względem
danej w postaci (1) definiuje się liczbę zespoloną sprzężoną względem 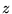 :
:
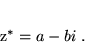 |
(3) |
Spełnione jest:
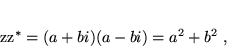 |
(4) |
a więc
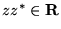 i
i 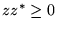 . Oczywiście,
. Oczywiście, 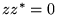 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
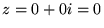 .
.
- Moduł liczby zespolonej
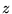 definiuje się jako
definiuje się jako
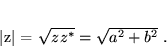 |
(5) |
Z powyższej definicji wynika, że 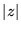 jest liczbą rzeczywistą nieujemną.
jest liczbą rzeczywistą nieujemną. 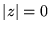 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 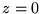 .
.
- Dla każdej liczby zespolonej
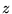 danej w postaci (1) definiuje się
danej w postaci (1) definiuje się
- część rzeczywistą 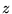 :
:
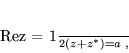 |
(6) |
- część urojoną 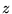 :
:
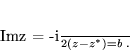 |
(7) |
Re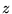 i Im
i Im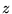 są więc liczbami rzeczywistymi.
są więc liczbami rzeczywistymi.
- Działania arytmetyczne w zbiorze liczb zespolonych: dla
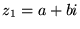 i
i
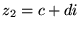 określa się:
określa się:
- sumę:
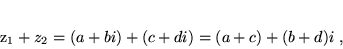 |
(8) |
- iloczyn:
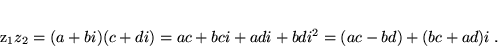 |
(9) |
Oba działania są przemienne. Dla każdej liczby zespolonej 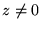 można skonstruować odwrotność
można skonstruować odwrotność 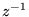 ,
,
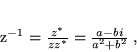 |
(10) |
tak, że zachodzi
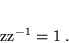 |
(11) |
Działania arytmetyczne w zbiorze liczb zespolonych są więc analogiczne do działań w zbiorze liczb rzeczywistych.
- Definicja liczby sprzężonej zespolonej (3), zastosowana do sumy i iloczynu liczb zespolonych, daje
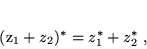 |
(12) |
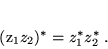 |
(13) |
Także w zastosowaniu do obliczania odwrotności otrzymujemy
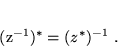 |
(14) |
- Dowodzi się, że
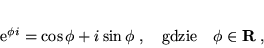 |
(15) |
- Liczba zespolona
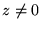 może być zapisana w tzw. postaci wykładniczej,
może być zapisana w tzw. postaci wykładniczej,
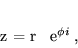 |
(16) |
oraz w równoważnej postaci trygonometrycznej:
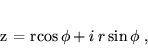 |
(17) |
gdzie 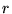 jest liczbą rzeczywistą nieujemną, a
jest liczbą rzeczywistą nieujemną, a
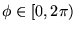 . łatwo sprawdzić, że
. łatwo sprawdzić, że
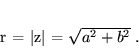 |
(18) |
Wielkość kątowa 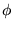 nazywana jest argumentem liczby
nazywana jest argumentem liczby 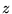 . Jest ona wyznaczona jako rozwiązanie układu równań
. Jest ona wyznaczona jako rozwiązanie układu równań
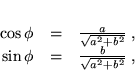 |
(19) |
należące do przedziału 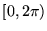 . Dla
. Dla 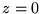 mamy
mamy 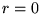 , a wartość
, a wartość 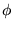 jest nieokreślona.
jest nieokreślona.
Postacie: wykładnicza i trygonometryczna liczby zespolonej 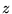 są wygodne przy obliczaniu potęg
są wygodne przy obliczaniu potęg 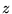 o dowolnym wykładniku całkowitym (dodatnim lub ujemnym), oraz ułamkowym (wyciąganie pierwiastków). W szczególności, odwrotność liczby
o dowolnym wykładniku całkowitym (dodatnim lub ujemnym), oraz ułamkowym (wyciąganie pierwiastków). W szczególności, odwrotność liczby 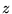 , patrz równ. (10), przedstawić można w postaciach:
, patrz równ. (10), przedstawić można w postaciach:
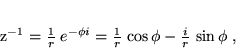 |
(20) |
które wynikają z równ. (15) i (16).
- Rozważmy wielomian stopnia
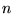 zmiennej zespolonej
zmiennej zespolonej 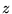 , o współczynnikach zespolonych:
, o współczynnikach zespolonych:
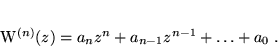 |
(21) |
Ważnym problemem jest określenie, czy taki wielomian ma pierwiastki (rozwiązania równania
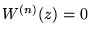 ). Tzw. podstawowe twierdzenie algebry glosi, źe wielomian (21) ma dokładnie
). Tzw. podstawowe twierdzenie algebry glosi, źe wielomian (21) ma dokładnie 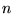 pierwiastków,
pierwiastków,
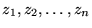 , (niekoniecznie różnych), tak, że możliwe jest przedstawienie iloczynowe:
, (niekoniecznie różnych), tak, że możliwe jest przedstawienie iloczynowe:
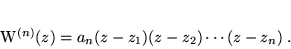 |
(22) |
Twierdzenie to nie zachodzi dla wielomianów zmiennej rzeczywistej. Np. wielomiany
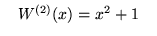 i
i
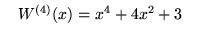 nie mają żadnych pierwiastków rzeczywistych.
nie mają żadnych pierwiastków rzeczywistych.
- Liczby zespolone spełniające warunek
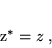 |
(23) |
(czyli liczby zespolone, których część urojona Im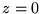 ) mają wszystkie własności arytmetyczne liczb rzeczywistych. Wygodnie będzie więc utożsamiać te liczby z liczbami rzeczywistymi. W tym sensie będziemy dalej uważać zbiór liczb rzeczywistych R za podzbiór zbioru liczb zespolonych C (co zapisuje się w postaci R
) mają wszystkie własności arytmetyczne liczb rzeczywistych. Wygodnie będzie więc utożsamiać te liczby z liczbami rzeczywistymi. W tym sensie będziemy dalej uważać zbiór liczb rzeczywistych R za podzbiór zbioru liczb zespolonych C (co zapisuje się w postaci R 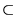 C), a równanie (23) za warunek definiujący liczbę rzeczywistą.
C), a równanie (23) za warunek definiujący liczbę rzeczywistą.
- Liczby zespolone spełniające warunek
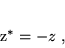 |
(24) |
(czyli liczby zespolone, których część rzeczywista Re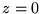 ) nazywane są liczbami urojonymi. Liczby te można zapisać w postaci
) nazywane są liczbami urojonymi. Liczby te można zapisać w postaci 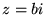 , gdzie
, gdzie 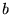 jest liczbą rzeczywistą. Suma dwóch liczb urojonych jest liczbą urojoną, ale iloczyn dwóch liczb urojonych jest zawsze liczbą rzeczywistą (ujemną).
jest liczbą rzeczywistą. Suma dwóch liczb urojonych jest liczbą urojoną, ale iloczyn dwóch liczb urojonych jest zawsze liczbą rzeczywistą (ujemną).
Edyta Malolepsza
2000-12-20