- Baza ortonormalna w przestrzeni wektorowej
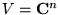 :
:
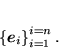 |
(72) |
- Rozwinięcie wektora
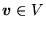 w bazie (72):
w bazie (72):
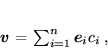 |
(73) |
gdzie
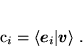 |
(74) |
- Operator liniowy działający w przestrzeni
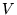 , wyrażony
przy użyciu bazy (72):
, wyrażony
przy użyciu bazy (72):
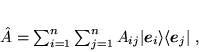 |
(75) |
gdzie współczynniki
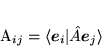 |
(76) |
tworzą macierz kwadratową 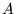 .
.
- Niech
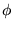 i
i 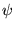 będą funkcjami porządnymi należącymi do przestrzeni Hilberta
będą funkcjami porządnymi należącymi do przestrzeni Hilberta 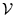 funkcji zespolonych zmiennej rzeczywistej
funkcji zespolonych zmiennej rzeczywistej ![$x \in [a,b]$](img217.png) . Iloczyn skalarny w przestrzeni
. Iloczyn skalarny w przestrzeni 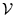 określony jest następująco:
określony jest następująco:
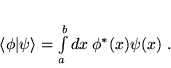 |
(77) |
Zadania
W zadaniach 1-3 przestrzeń wektorowa 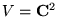 .
.
-
Dana jest macierz
Jakie warunki spełniać muszą liczby 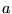 ,
, 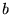 ,
, 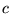 i
i 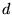 , aby odpowiadający tej macierzy operator
, aby odpowiadający tej macierzy operator 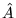 , dany w postaci (75), był hermitowski? Sprawdzić poprawność znalezionych warunków przez obliczenie iloczynów skalarnych
, dany w postaci (75), był hermitowski? Sprawdzić poprawność znalezionych warunków przez obliczenie iloczynów skalarnych
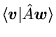 i
i
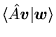 , gdzie
, gdzie
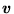 i
i
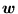 są dowolnymi wektorami wyrażonymi w postaci (73).
są dowolnymi wektorami wyrażonymi w postaci (73).
-
Pewnemu operatorowi
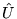 danemu w postaci (75) odpowiada macierz
danemu w postaci (75) odpowiada macierz
Wykazać, że macierz
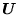 jest unitarna. Obliczając iloczyny skalarne
jest unitarna. Obliczając iloczyny skalarne
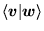 i
i
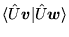 , gdzie
, gdzie
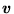 i
i
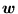 są dowolnymi wektorami wyrażonymi w postaci (73), pokazać, że operator
są dowolnymi wektorami wyrażonymi w postaci (73), pokazać, że operator 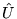 jest unitarny.
jest unitarny.
-
Wektory
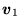 i
i
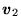 dane są w postaci (73), a odpowiadające im współczynniki rozwinięcia zapisane są w postaci następujących macierzy jednokolumnowych:
dane są w postaci (73), a odpowiadające im współczynniki rozwinięcia zapisane są w postaci następujących macierzy jednokolumnowych:
gdzie 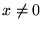 jest liczbą rzeczywistą. Sprawdzić, że
jest liczbą rzeczywistą. Sprawdzić, że
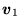 i
i
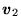 są wektorami własnymi operatora
są wektorami własnymi operatora 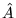 z zad. 1, gdzie w macierzy
z zad. 1, gdzie w macierzy
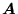 położono
położono 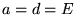 i
i 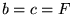 , a
, a 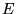 i
i 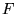 są liczbami rzeczywistymi. Znaleźć wartości własne
są liczbami rzeczywistymi. Znaleźć wartości własne 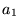 i
i 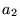 tego operatora
tego operatora 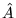 , odpowiadające wektorom
, odpowiadające wektorom
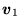 i
i
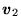 . Znormalizować wektory
. Znormalizować wektory
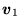 i
i
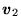 i sprawdzić, że uzyskany zbiór wektorów własnych tworzy bazę ortonormalną w przestrzeni wektorowej
i sprawdzić, że uzyskany zbiór wektorów własnych tworzy bazę ortonormalną w przestrzeni wektorowej
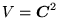 . Oznaczając przez
. Oznaczając przez 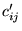 odpowiednie współczynniki unormowanych wektorów własnych, pokazać, że macierz
odpowiednie współczynniki unormowanych wektorów własnych, pokazać, że macierz
jest macierzą unitarną.
-
Rozwaźamy zbiór wszystkich funkcji zmiennej rzeczywistej
![$x \in [-\pi, \pi]$](img246.png) , które wyrazić można w postaci kombinacji liniowych
, które wyrazić można w postaci kombinacji liniowych
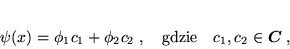 |
(78) |
gdzie
Pokazać, że funkcje (78) tworzą dwuwymiarową zespoloną przestrzeń wektorową. Przyjmując, że iloczyn skalarny w tej przestrzeni dany jest w postaci (77), pokazać, że funkcje 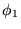 i
i 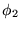 , po znormalizowaniu, tworzą w tej przestrzeni bazę ortonormalną.
Pokazać, źe operator różniczkowania,
, po znormalizowaniu, tworzą w tej przestrzeni bazę ortonormalną.
Pokazać, źe operator różniczkowania,
jest operatorem liniowym w rozważanej przestrzeni wektorowej. Wyznaczyć macierz
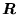 tego operatora w bazie ortonormalnej. Dla jakich
tego operatora w bazie ortonormalnej. Dla jakich 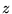 operator
operator 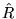 jest operatorem hermitowskim w tej przestrzeni wektorowej?
jest operatorem hermitowskim w tej przestrzeni wektorowej?
Edyta Malolepsza
2000-12-20