Macierze
Macierzą  o wymiarach
o wymiarach 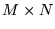 nazywa się zbiór pewnych elementów
nazywa się zbiór pewnych elementów
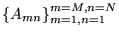 , ułożonych w formie dwuwymiarowej tablicy:
, ułożonych w formie dwuwymiarowej tablicy:
 |
(25) |
Gdy 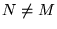 , macierz taką nazywamy macierzą prostokątną, a gdy
, macierz taką nazywamy macierzą prostokątną, a gdy 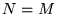 , macierzą kwadratową. Pierwszy wskaźnik,
, macierzą kwadratową. Pierwszy wskaźnik,
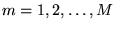 , numeruje wiersze macierzy, a drugi wskaźnik,
, numeruje wiersze macierzy, a drugi wskaźnik,
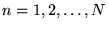 , numeruje kolumny macierzy. Gdy
, numeruje kolumny macierzy. Gdy 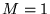 , macierz nazywa się macierzą (jedno)wierszową, a gdy
, macierz nazywa się macierzą (jedno)wierszową, a gdy 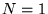 , macierzą (jedno)kolumnową; takie macierze będą dalej oznaczane małymi literami pogrubionymi, np.
, macierzą (jedno)kolumnową; takie macierze będą dalej oznaczane małymi literami pogrubionymi, np.
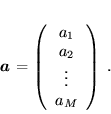 |
(26) |
oznacza macierz kolumnową, gdzie dla wygody pominięto drugi wskaźnik (zawsze równy 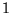 ), np.
), np.
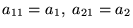 , itd. Elementy macierzy,
, itd. Elementy macierzy, 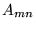 , są zwykle liczbami należącymi do pewnego zbioru K, gdzie K
, są zwykle liczbami należącymi do pewnego zbioru K, gdzie K 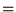 R lub K
R lub K 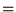 C. Zgodnie z uwagą 9 rozdziału 1 przyjmujemy, że R
C. Zgodnie z uwagą 9 rozdziału 1 przyjmujemy, że R 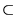 C, i będziemy traktować przypadek K
C, i będziemy traktować przypadek K 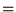 R jako przypadek szczególny sytuacji ogólnej K
R jako przypadek szczególny sytuacji ogólnej K  C.
C.
- Równość dwu macierzy,
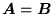 , zachodzi, gdy mają te same wymiary i ich odpowiednie elementy są równe:
, zachodzi, gdy mają te same wymiary i ich odpowiednie elementy są równe:
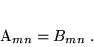 |
(27) |
- Dodawanie macierzy jest określone dla macierzy o tych samych wymiarach
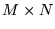 :
:
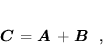 |
(28) |
gdy elementy macierzy 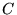 wyznaczone są w postaci:
wyznaczone są w postaci:
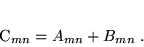 |
(29) |
Dodawanie macierzy jest przemienne. Istnieje macierz zerowa 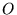 (o elementach równych 0), taka, źe dla dowolnej macierzy
(o elementach równych 0), taka, źe dla dowolnej macierzy 
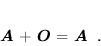 |
(30) |
Dla każdej macierzy  istnieje macierz przeciwna
istnieje macierz przeciwna 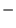
 (o elementach przeciwnych, równych
(o elementach przeciwnych, równych 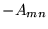 ), tak, że zachodzi
), tak, że zachodzi
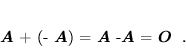 |
(31) |
Można też zdefiniować mnożenie macierzy przez liczbę:
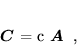 |
(32) |
gdy elementy macierzy 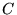 wyznaczone są w postaci:
wyznaczone są w postaci:
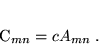 |
(33) |
- Niech
 jest macierzą o wymiarach
jest macierzą o wymiarach 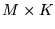 , a
, a 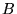 macierzą o wymiarach
macierzą o wymiarach 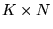 . Iloczynem tych macierzy nazywamy macierz
. Iloczynem tych macierzy nazywamy macierz 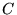 o wymiarach
o wymiarach 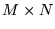 ,
,
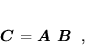 |
(34) |
której elementy oblicza się w sposób następujący:
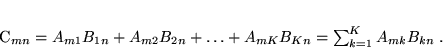 |
(35) |
Można powiedzieć, że element 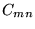 powstaje w wyniku ''pomnożenia''
powstaje w wyniku ''pomnożenia'' 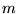 -tego wiersza macierzy
-tego wiersza macierzy  przez
przez 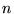 -tą kolumnę macierzy
-tą kolumnę macierzy 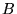 .
.
- Gdy macierze
 ,
, 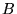 są macierzami kwadratowymi o wymiarach
są macierzami kwadratowymi o wymiarach 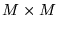 , ich iloczyny
, ich iloczyny 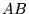 i
i 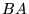 są także macierzami kwadratowymi o tych wymiarach i, naogół,
są także macierzami kwadratowymi o tych wymiarach i, naogół,
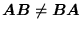 . W zbiorze macierzy kwadratowych, oprócz działań opisanych w p. 2, jest więc określone mnożenie (nieprzemienne). Z definicji dodawania (29) i mnożenia macierzy (35) wynika, że zachodzi rozdzielność dodawania względem mnożenia:
. W zbiorze macierzy kwadratowych, oprócz działań opisanych w p. 2, jest więc określone mnożenie (nieprzemienne). Z definicji dodawania (29) i mnożenia macierzy (35) wynika, że zachodzi rozdzielność dodawania względem mnożenia:
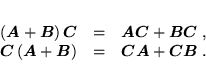 |
(36) |
- Mając daną macierz zespoloną
 o wymiarach
o wymiarach 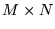 , można skonstruować pewne macierze z nią związane:
, można skonstruować pewne macierze z nią związane:
- Macierz zespolona sprzężona
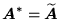 , o takich samych wymiarach i o elementach sprzężonych zespolonych,
, o takich samych wymiarach i o elementach sprzężonych zespolonych,
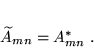 |
(37) |
- Macierz transponowaną
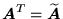 , o wymiarach
, o wymiarach 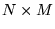 i elementach
i elementach
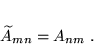 |
(38) |
Macierz transponowana
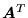 powstaje z macierzy
powstaje z macierzy  przez zamianę wierszy na kolumny i kolumn na wiersze, z pozostawieniem na miejscu tzw. elementów diagonalnych:
przez zamianę wierszy na kolumny i kolumn na wiersze, z pozostawieniem na miejscu tzw. elementów diagonalnych:
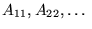 .
.
- Macierz hermitowsko sprzężoną
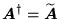 , o wymiarach
, o wymiarach 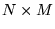 i elementach
i elementach
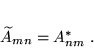 |
(39) |
Zachodzi oczywiście
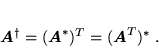 |
(40) |
Na przykład, macierz hermitowsko sprzężona względem macierzy kolumnowej 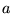 , patrz równ. (26), jest macierzą wierszową:
, patrz równ. (26), jest macierzą wierszową:
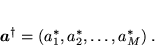 |
(41) |
Zauważmy przy okazji, że mnożenie macierzy wierszowej 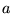
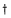 przez macierz kolumnową
przez macierz kolumnową 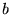 , analogiczną do macierzy (26), daje macierz
, analogiczną do macierzy (26), daje macierz 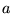
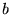 , która jest macierzą o wymiarach
, która jest macierzą o wymiarach 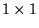 , czyli pewną liczbą ze zbioru liczb K:
, czyli pewną liczbą ze zbioru liczb K:
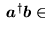 K.
K.
Dwukrotne powtórzenie każdej z operacji (a-c) przywraca stan początkowy:
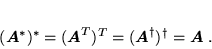 |
(42) |
Zastosowanie operacji (a-c) do sumy macierzy daje:
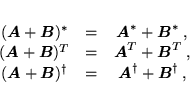 |
(43) |
a w przypadku iloczynu macierzy przez liczbę:
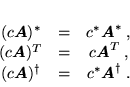 |
(44) |
Z kolei, zastosowanie operacji (a-c) do iloczynu macierzy daje:
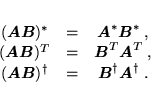 |
(45) |
Odnotujmy zmianę porządku iloczynu w wyniku operacji (b) i (c).
- Szczególną rolę w algebrze odgrywają macierze kwadratowe (
 ). Wśród macierzy kwadratowych wyróżnioną role odgrywają: (kwadratowa) macierz zerowa
). Wśród macierzy kwadratowych wyróżnioną role odgrywają: (kwadratowa) macierz zerowa  , o własnościach określonych w równ. (30) i (31), oraz macierz jednostkowa,
, o własnościach określonych w równ. (30) i (31), oraz macierz jednostkowa,
 |
(46) |
spełniająca rolę ''jedynki'' w mnożeniu macierzy:
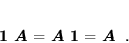 |
(47) |
- Każdej macierzy kwadratowej
 można przypisać liczbę
można przypisać liczbę
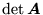 , zwaną wyznacznikiem macierzy
, zwaną wyznacznikiem macierzy  , zapisywaną także jako
, zapisywaną także jako
 |
(48) |
a zdefinowaną formalnie w postaci
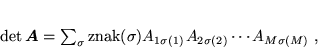 |
(49) |
gdzie sumowanie rozciąga się na wszystkie 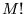 permutacji zbioru wskaźników
permutacji zbioru wskaźników 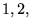
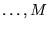 numerujących kolumny macierzy
numerujących kolumny macierzy  , a znak(
, a znak(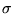 ) jest znakiem permutacji
) jest znakiem permutacji 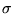 , przyjmującym wartości
, przyjmującym wartości 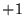 lub
lub 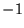 , w zależności od tego, czy permutacja ta jest parzysta, czy nieparzysta. Prosty przykład: wyznacznik macierzy
, w zależności od tego, czy permutacja ta jest parzysta, czy nieparzysta. Prosty przykład: wyznacznik macierzy  o wymiarach
o wymiarach 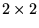 :
:
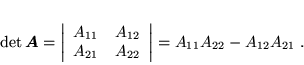 |
(50) |
W przypadku macierzy wyższych wymiarów efektywnym sposobem obliczania wyznaczników jest zastosowanie tzw. rozwinięcia Laplace'a (względem kolumn lub wierszy macierzy). Niektóre własności wyznacznika macierzy:
- Jeśli z macierzy
 utworzyć nową macierz
utworzyć nową macierz
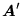 przez zamianę dwóch kolumn (lub dwóch wierszy), to
przez zamianę dwóch kolumn (lub dwóch wierszy), to
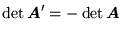 . Wynika stąd, że gdy dwie kolumny (lub dwa wiersze) macierzy
. Wynika stąd, że gdy dwie kolumny (lub dwa wiersze) macierzy  są identyczne, to
są identyczne, to
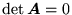 .
.
- Zachodzi
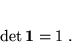 |
(51) |
Dla każdej macierzy kwadratowej  mamy
mamy
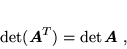 |
(52) |
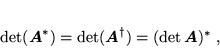 |
(53) |
- Jeśli macierze
 i
i 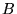 są macierzami kwadratowymi o tych samych wymiarach, to
są macierzami kwadratowymi o tych samych wymiarach, to
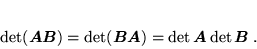 |
(54) |
- Jeśli
 jest macierzą kwadratową i
jest macierzą kwadratową i
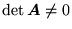 , to istnieje macierz odwrotna do macierzy
, to istnieje macierz odwrotna do macierzy  , oznaczana przez
, oznaczana przez
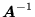 , taka, że
, taka, że
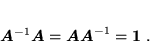 |
(55) |
Z równ. (51), (54) i (55) wynika, że
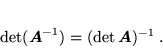 |
(56) |
Prosty przykład: macierz odwrotna do macierzy  o wymiarach
o wymiarach 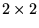 :
:
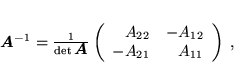 |
(57) |
gdzie
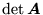 jest zdefiniowany w równ. (50).
jest zdefiniowany w równ. (50).
Jeśli  i
i 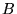 są macierzami kwadratowymi o tych samych wymiarach i są odwracalne (czyli mają odwrotności), to ich iloczyn
są macierzami kwadratowymi o tych samych wymiarach i są odwracalne (czyli mają odwrotności), to ich iloczyn 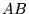 jest także macierzą odwracalną [bo wyznacznik (54) jest różny od zera] i zachodzi
jest także macierzą odwracalną [bo wyznacznik (54) jest różny od zera] i zachodzi
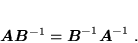 |
(58) |
Tu, podobnie jak w przypadku operacji (b) i (c) w równ. (45), także zachodzi zmiana porządku iloczynu.
- Rozważmy macierze zespolone (K
 C). Macierz kwadratową
C). Macierz kwadratową  nazywamy:
nazywamy:
- rzeczywistą, gdy
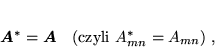 |
(59) |
- symetryczną, gdy
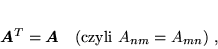 |
(60) |
- hermitowską, gdy
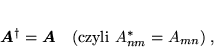 |
(61) |
- ortogonalną, gdy
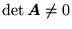 i zachodzi
i zachodzi
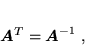 |
(62) |
- unitarną, gdy
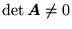 i zachodzi
i zachodzi
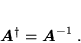 |
(63) |
Z równ. (52), (56) i (62) wynika, źe w przypadku macierzy ortogonalnej zachodzi
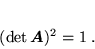 |
(64) |
Podobnie, z równ. (53), (56) i (63) wynika, źe w przypadku macierzy unitarnej zachodzi
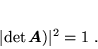 |
(65) |
Gdy rozważamy macierze rzeczywiste (K 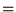 R), to równ. (59) jest zawsze spełnione, patrz uwaga 9 w rozdziale 1. W tym przypadku pojęcie macierzy hermitowskiej pokrywa się z pojęciem macierzy symetrycznej, a pojęcie macierzy unitarnej pokrywa się z pojęciem macierzy ortogonalnej.
R), to równ. (59) jest zawsze spełnione, patrz uwaga 9 w rozdziale 1. W tym przypadku pojęcie macierzy hermitowskiej pokrywa się z pojęciem macierzy symetrycznej, a pojęcie macierzy unitarnej pokrywa się z pojęciem macierzy ortogonalnej.
Edyta Malolepsza
2000-12-20
