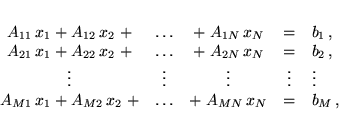Układ 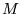 równań liniowych z
równań liniowych z 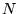 niewiadomymi
niewiadomymi
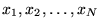 , należącymi do zbioru liczb K (równego R lub C), zapisuje się w postaci
, należącymi do zbioru liczb K (równego R lub C), zapisuje się w postaci
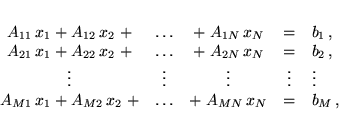 |
(66) |
gdzie liczby 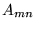 , zwane współczynnikami liniowymi, tworzą macierz prostokątną
, zwane współczynnikami liniowymi, tworzą macierz prostokątną 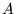 o wymiarach
o wymiarach 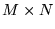 , patrz równ. (25), a liczby
, patrz równ. (25), a liczby 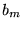 , zwane wyrazami wolnymi, tworzą macierz kolumnową
, zwane wyrazami wolnymi, tworzą macierz kolumnową 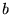 o wymiarze
o wymiarze 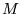 , analogiczną do zdefiniowanej w równ. (26). Zarówno współczynniki liniowe, jak i wyrazy wolne należą do tego samego zbioru liczb K. Wprowadzając macierz kolumnową o wymiarze
, analogiczną do zdefiniowanej w równ. (26). Zarówno współczynniki liniowe, jak i wyrazy wolne należą do tego samego zbioru liczb K. Wprowadzając macierz kolumnową o wymiarze 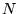 , zbudowaną z niewiadomych,
, zbudowaną z niewiadomych,
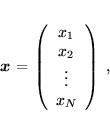 |
(67) |
można układ równań (66) zapisać w równoważnej postaci macierzowej:
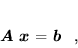 |
(68) |
gdzie mnożenie macierzy współczynników 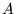 , o wymiarach
, o wymiarach 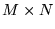 , przez macierz niewiadomych
, przez macierz niewiadomych 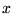 , o wymiarach
, o wymiarach 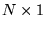 , daje macierz wyrazów wolnych
, daje macierz wyrazów wolnych 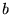 , o wymiarach
, o wymiarach 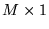 .
.
- Układ równań liniowych (66) może: (i) nie mieć rozwiązań (nazywany jest wtedy sprzecznym), (ii) mieć jedno rozwiązanie
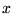 , (iii) mieć nieskończenie wiele rozwiązań.
, (iii) mieć nieskończenie wiele rozwiązań.
- Układ równań liniowych (66) nazywa się układem jednorodnym, gdy wszystkie wyrazy wolne są równe zeru,
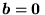 ; w przeciwnym wypadku układ nazywa się układem niejednorodnym. Jednym z rozwiązań jednorodnego układu równań liniowych jest zawsze rozwiązanie zerowe,
; w przeciwnym wypadku układ nazywa się układem niejednorodnym. Jednym z rozwiązań jednorodnego układu równań liniowych jest zawsze rozwiązanie zerowe,
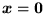 . Uwaga: jeśli
. Uwaga: jeśli
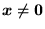 jest rozwiązaniem jednorodnego układu równań, a
jest rozwiązaniem jednorodnego układu równań, a 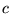 jest dowolną liczbą ze zbioru K, to
jest dowolną liczbą ze zbioru K, to
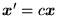 jest także rozwiązaniem tego układu równań.
jest także rozwiązaniem tego układu równań.
- Dowodzi się, że jeśli w układzie równań (66):
(a) jedno z równań-wierszy pomnożyć stronami przez pewną liczbę 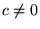 , to otrzymany w ten sposób nowy układ równań ma ten sam zbiór rozwiązań;
, to otrzymany w ten sposób nowy układ równań ma ten sam zbiór rozwiązań;
(b) do jednego z równań-wierszy dodać stronami inne równanie-wiersz, to otrzymany w ten sposób nowy układ równań ma ten sam zbiór rozwiązań.
Wielokrotne zastosowanie operacji (a) i (b), z odpowiednio dobranymi mnożnikami 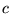 , może doprowadzic do eliminacji jednej z niewiadomych, a w konsekwencji do otrzymania nowego układu
, może doprowadzic do eliminacji jednej z niewiadomych, a w konsekwencji do otrzymania nowego układu 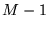 równań z
równań z 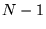 niewiadomymi; jest to metoda rozwiązywania układu równań liniowych przez kolejną eliminację niewiadomych.
niewiadomymi; jest to metoda rozwiązywania układu równań liniowych przez kolejną eliminację niewiadomych.
- Skupimy się teraz na ważnym przypadku szczególnym, gdy liczba równań równa jest liczbie niewiadomych,
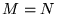 . Macierz
. Macierz 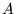 jest wtedy macierzą kwadratową
jest wtedy macierzą kwadratową 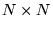 . Rozpatrzymy dwie możliwości:
. Rozpatrzymy dwie możliwości:
(1)
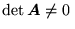 . Istnieje wtedy macierz odwrotna
. Istnieje wtedy macierz odwrotna
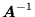 , i mnożąc lewostronnie obie strony równania macierzowego (68) przez tę macierz otrzymujemy (jedyne) rozwiązanie układu równań (66) w postaci
, i mnożąc lewostronnie obie strony równania macierzowego (68) przez tę macierz otrzymujemy (jedyne) rozwiązanie układu równań (66) w postaci
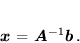 |
(69) |
Metoda rozwiązywania układu równań liniowych 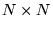 przez wyznaczanie macierzy
przez wyznaczanie macierzy
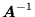 nie jest opłacalna w praktyce, gdy liczba niewiadomych
nie jest opłacalna w praktyce, gdy liczba niewiadomych 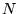 jest duża; korzystniej jest wtedy stosować odpowiednio zoptymalizowaną metodę kolejnej eliminacji niewiadomych. W szczególnym przypadku jednorodnego układu równań,
jest duża; korzystniej jest wtedy stosować odpowiednio zoptymalizowaną metodę kolejnej eliminacji niewiadomych. W szczególnym przypadku jednorodnego układu równań,
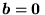 , z równ. (69) otrzymujemy jako (jedyne) rozwiązanie wynik
, z równ. (69) otrzymujemy jako (jedyne) rozwiązanie wynik
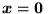 .
.
(2)
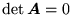 . W tym przypadku można wykazać, że niejednorodny układ równań (66) jest albo sprzeczny, albo ma nieskończenie wiele rozwiązań.
Interesujący jest przypadek układu jednorodnego - można wykazać, że taki układ ma w tym przypadu także rozwiązania niezerowe,
. W tym przypadku można wykazać, że niejednorodny układ równań (66) jest albo sprzeczny, albo ma nieskończenie wiele rozwiązań.
Interesujący jest przypadek układu jednorodnego - można wykazać, że taki układ ma w tym przypadu także rozwiązania niezerowe,
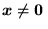 . Co więcej, jest wtedy nieskończenie wiele rozwiązań niezerowych proporcjonalnych do siebie, patrz uwaga w punkcie 2. Mogą jednak wystąpić także rozwiązania niezerowe, które nie są proporcjonalne do siebie. łatwo można wykazać, że jeśli
. Co więcej, jest wtedy nieskończenie wiele rozwiązań niezerowych proporcjonalnych do siebie, patrz uwaga w punkcie 2. Mogą jednak wystąpić także rozwiązania niezerowe, które nie są proporcjonalne do siebie. łatwo można wykazać, że jeśli
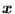 i
i
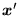 są takimi dwoma rozwiązaniami, to
są takimi dwoma rozwiązaniami, to
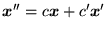 , gdzie
, gdzie 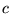 i
i 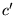 są dowolnymi liczbami ze zbioru K, jest także rozwiązaniem niezerowym naszego jednorodnego układu równań liniowych.
Podumowując: warunkiem koniecznym i wystarczającym, by jednorodny układ N równań liniowych z N niewiadomymi (66) miał rozwiązania niezerowe, jest
są dowolnymi liczbami ze zbioru K, jest także rozwiązaniem niezerowym naszego jednorodnego układu równań liniowych.
Podumowując: warunkiem koniecznym i wystarczającym, by jednorodny układ N równań liniowych z N niewiadomymi (66) miał rozwiązania niezerowe, jest
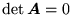 .
.
Edyta Malolepsza
2000-12-20